
Každá položka na této stránce byla ručně vybrána editorem House Beautiful. Můžeme vydělat provizi za některé položky, které se rozhodnete koupit.
Není nic jako šílený matematický problém, optická iluze ohýbající mysl, nebo kroucená logická hádanka zastavit veškerou produktivitu na internetu Populární mechanika kancelář. Jsme zvědaví lidé od přírody, ale také společně sdílíme tvrdohlavé naléhání, které jsme správně, sakra, a tak máme sklon házet práci po boku, kdykoli narazíme na problém s několika zdánlivě možnými řešeními.
Tento trojúhelníkový hlavolam není nový - výkřiky Popsugar pro odkrýt to před pár lety - ale na základě nějaké stinné internetové magie se níže uvedený tweet v mém zdroji znovu objevil a začal novou debatu o našich zaměstnancích Slack kanál, místo tradičně vyhrazené pro nápady na workshop, ale místo toho se většinou používá k řvát na další věci, na které se občas proměníme obsah.
Říci? pic.twitter.com/lrhXrWw5EP
- J (@jiteshpillaai) 9. dubna 2018
Protože jsem masochista, znovu jsem nakreslil trojúhelník a požádal všechny zaměstnance, aby okamžitě upustili od toho, co dělali, a pokusili se vyřešit jednoduchou otázku: Kolik trojúhelníků můžete najít?
Ušetřím ti celou konverzaci - věř mi, nikdo to nechce vidět - ale reakce týmu se pohybovala všude. Někteří editoři viděli čtyři trojúhelníky. Ostatní viděli 12. Několik jich vidělo 6, 16, 22. Ještě více viděl 18. Jeden wiseguy počítal trojúhelníky v A v samotné otázce, zatímco jiný vypadal, že má existenciální krize: „Žádná z těchto linií není skutečně přímá, pouze křivky - tedy nelze definovat žádnou z nich jako trojúhelník,“ řekl. "Na této fotografii nejsou žádné trojúhelníky." Život nemá smysl. “
Poté jsme problém položili našim stoupencům Instagramu, jejichž odpovědi také spustili gamut, od 5 do 14 do 37. I když uznáváme vysokou pravděpodobnost trollingu zde, je jasné, že lidé reagují na problém mnoha různými způsoby.
Zobrazit tento příspěvek na Instagramu
Zastavte prosím to, co děláte, a pomozte nám vyřešit rozpravu, kterou právě vedeme v kanceláři. Kolik trojúhelníků vidíte zde?
Příspěvek sdílený uživatelem Populární časopis Mechanics (@popularmechanics)
Celou dobu jsem poslouchal, jak kolegové vysvětlují své pochybné procesy, ale místo toho jsem oslovil několik odborníků na geometrii, abych zjistil, zda bychom mohli dospět ke konsensuální odpovědi. Ukázalo se, že prakticky všichni matematici, se kterými jsem kontaktoval, našli stejné řešení - ale ne všichni z nich na to přišli stejným způsobem.
Pokud ještě nechcete znát odpověď, přestaňte číst a pokuste se problém nejprve vyřešit. Až skončíte, setkám se s vámi.
Hej, to bylo rychlé. Jste připraveni na odpověď? Na rozdíl od některých virové matematické problémy které jsou záměrně neurčité a otevřené pro interpretaci, toto vlastně má řešení slam-dunk, nepochybně o tom, a je to 18. Řekněme si od některých odborníků na geometrii, proč.
"K tomu bych přistupoval stejně jako k matematickému problému: omezte jej a najděte strukturu," říká Sylvester Eriksson-Bique, Ph. D., postdoktorandka z matematiky University of California v Los Angeles oddělení.
Erikkson-Bisque říká, že jediný způsob, jak vytvořit trojúhelníky, je, že horní vrchol (roh) je součástí trojúhelníku. Základna trojúhelníku bude potom muset být jednou ze tří úrovní níže. "Existují tři úrovně a na každé si můžete vybrat základnu mezi šesti různými způsoby." To dává 18 nebo 3 krát 6 trojúhelníků. “
Podívejme se znovu na hlavní trojúhelník.

Andrew Daniels
"Je vhodné zobecnit na případ, kdy existují." n - linie procházející horním vrcholem a - str vodorovné čáry, “říká Francis Bonahon, Ph. D., profesor matematiky na University of Southern California.
V našem případě, n = 4 a p = 3. Jakýkoli trojúhelník, který najdeme ve výkresu, by měl mít jeden horní vrchol a dva další na stejné horizontální linii, takže pro každou horizontální linii by měl být počet trojúhelníků s dva vrcholy na této lince se rovnají počtu způsobů, jak si můžeme tyto vrcholy vybrat, říká Bonahon - konkrétně počet způsobů, jak si můžeme vybrat dva odlišné body z nnebo „n zvolte 2. “
Pamatujete si matematiku na střední škole? To je n(n-1)/2. A protože tam jsou str vodorovné čáry, říká Bonahan, to dává p n(n-1) / 2 možné trojúhelníky. V našem případě je to 3x4 (4-1) / 2 = 18.
Zde je užitečný přehled toho, jak najít každý možný trojúhelník:

Kory Kennedyová
Johanna Mangahas, Ph. D., pomocná profesorka matematiky na univerzitě v Buffalu, také přišla na 18 let - nejprve prostým počítáním hrubou silou, poté stejnou lstivostí Combinatorics, jak je uvedeno výše - ale připouští, že náš trojúhelníkový hlavolam není tak cool jako tenhle z Po-Shen Loh, Ph. D., profesora matematiky na Carnegie Mellon University v Pittsburgh, as vystupoval v New York Timesminulý rok:

Po-Shen Loh
Ten má úhlednější matematickou odpověď, říká, protože zde je počítání trojúhelníků stejné jako počítání kombinací tří řádků vybraných ze šesti [6-select-3 = (6 * 5 * 4) / (3 * 2 *) 1)].
"V takovém případě se každá dvojice čar protíná a neexistují žádné trojité nebo více křižovatek, takže každá ze tří možností vždy dává trojúhelník," říká Mangahas. Na obrázku, který jsem jí poslal, jsou některé čáry rovnoběžné, takže nemohou být součástí stejného trojúhelníku. "Pokud jste vzali stejných sedm řádků a trochu je zatřásli, pravděpodobně by to nejspíš byli." přistát jako [Lohův] problém a měli byste více trojúhelníků a podobnou roztomilý odpověď. “(Pro záznam: 35.)
Whew. Tento nový problém s trojúhelníkem jsem dosud nesdělil se svými spolupracovníky. Ale je jen otázkou času, než to zjistí - a argumentují ještě víc.
🚨DŮLEŽITÁ AKTUALIZACE 1/30/20🚨: Od vydání tohoto příběhu mnoho mnoho čtenáři oslovili, aby mi dali vědět, že zatímco 18 je skutečně přijatelnou odpovědí na tento problém, není to pouze jeden, kvůli nějakému neúmyslnému dohledu z mé strany. Mohl jsem to usnadnit čtenářům - a hlavně mnohem jednodušší ve své doručené poště - kdybych jen nakreslil trojúhelník na obyčejný bílý počítačový papír. Ale ne.
Bohužel jsem tento trojúhelník nakreslil na linkovaný papír a mnoho inteligentních lidí na to správně poukázalo, vlastně, pokud počítáte světle modré rovnoběžné čáry v obraze kromě tmavě modrých čar zapsaných v značce, je zde skutečně více než 18 trojúhelníků celkem - podstatně více. Nikdy jsem neurčil použít pouze tyto tmavě modré čáry, a tak se mýlím. Máš pravdu.
Jeden čtenář, Ralph Linsangan, mě naprosto vlastnil zasláním tohoto obrázku, ve kterém označil každý další trojúhelník nalezený podle technické specifikace a označil 17 dalších trojúhelníků celkem 35. Spatřit:
Tento druh obětavosti je jen jedním z mnoha důvodů, které miluji Populární mechanika čtenáři. Nemůžeme dostat nic za vás. Až do dalšího teaseru!
🚨DALŠÍ DŮLEŽITÉ AKTUALIZACE 1/31 / 20🚨: Od zveřejnění poslední aktualizace jsem slyšel od sudého více tebe, pokračoval v pronásledování mě - a vašich kolegů čtenářů - za to, že nebrali v úvahu další možné trojúhelníky. Slyšíme od čtenáře Dereka Schneidera, který poslal další grafiku, která naznačuje, že je 45 trojúhelníků.
Pokud však budeme dodržovat původní pravidla, počítám a dalších 9, které jsou definitivní (zeleně) a které by mohly být otevřený interpretaci v závislosti na tom, jak vizuálně umístíte vrcholový vrchol (purpurově)… osobně bych počítal to.
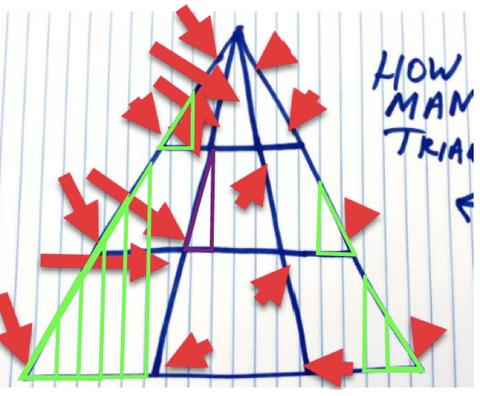
Derek Schneider
Čtenář Mezitím napsal, že jsme udělali „závažnou chybu“ v počítání trojúhelníků po celou dobu:
Vezměte například pravý dolní roh, například ukazuje jednu šipku pro jeden trojúhelník. Tyto světle modré čáry by však mohly tvořit až tři trojúhelníky v tomto jediném rohu:

Poingly
Zatímco některé z nich MŮŽE být poněkud diskutabilní (tj. Kde EXACTLY světelné modré čáry protínají tmavé a dělají technicky tvoří trojúhelník nebo čtyřúhelník), počítal jsem sedm dalších trojúhelníků, které mohou být v tomto cesta. Tím se celkový počet trojúhelníků zvýší na 42.
Špatnou zprávou je, že nám chyběly některé trojúhelníky. Dobrou zprávou je, že to potvrzuje, že život jasně nemá smysl, jak dokazuje přesné číslo: 42.
Vynikající bod, Poingly. Čtenář James Goodrich to udělal ještě o krok dále a navrhl, abychom otevřeli naši mysl a zvážili, jaký by trojúhelník mohl být:
Podle tvého čtenáře, který poukázal na dalších 17 trojúhelníků, použil „Andrew ne určit, jaké řádky mohou obsahovat 3 okraje trojúhelníkové klauzule), nepodařilo se jim najít docela dost více. Vezměte si například v levém dolním rohu trojúhelník v dodatku „Důležitá aktualizace“ z 30. ledna 2020. Nepomohly by oblasti mini-trojúhelníku a oblasti kosočtverce, které k němu sousedí, dohromady další trojúhelník?
Další nápad k uvážení: Trojúhelníky mají 3 úhly (kdo by to uhodl?); nicméně bych předpokládal, že jak budete popisovat trojúhelník, pomocí řečených úhlů, generujete různé trojúhelníky. Vzhledem k trojúhelníku T se vrcholy A, B a C by t-one mohl být ve skutečnosti popsán ABC, přičemž B je středový úhel. Navrhuji, aby t-dva, které popisuje BAC, byly odlišné. Podobně pro BCA.
Pokud tedy vezmeme konkrétní případ, pravoúhlé trojúhelníky, můžeme odvodit sinusové, kosinové a tečné funkce (SOH, CAH, TOA). Pokud bychom to měli aplikovat na trojúhelník (a uvolnit požadavek na pravý úhel, mohlo by to znamenat, že BAC je jiný než CAB. Výjimky jsou samozřejmě pro isoscolese a rovnostranné trojúhelníky (ty by měly pouze 3 odlišné definice trojúhelníku).
Ještě jsem docela nepřemýšlel o tom, jak kvantifikovat každý návrh (a jeho použití po prvním by zvýšilo počet stále), takže pro vás nemám snadné číslo, které byste mohli použít v aktualizované důležité aktualizaci (pokud jste zjistili, že má myšlenka stojí za to Aktualizace).
Ano, Jamesi. A budu čekat. Naštěstí jsem se rozhodl vzít poslední bod, abych zjistil, kolik dalších trojúhelníků by mohlo být dáno našim novým chaotickým pravidlům, a dospěl k 43, celkem 61:

Andrew Daniels
Jsem si však zcela jistý, že někdo, kdo si to přečte, mi velmi rychle řekne, že se ještě jednou mýlím a předložím důkaz ještě více skrytých trojúhelníků, které mě posílaly dolů po další králičí díře na dlouhé a klikaté cestě k případnému šílenství. (Vedlejší poznámka: Neviděl jsem svou ženu za tři dny. Řekněte jí, že ji miluji.) Vydávám tedy poslední výzvu: Pokud v původním obrázku najdete co nejvíce trojúhelníků, ukažte mi svoji práci a definitivně dokažte Vaše svrchovanost, tento příběh aktualizuji ještě jednou a korunuji vás králem nebo trojúhelníkem trojúhelníku, nyní a navždy. Pozdrav na rozloučenou.

SpeedRipper Rubikova kostka
$12.45
Rubikova kostka šílí lidi už 40 let. Zkuste na to přijít sami, nebo Naučte se, jak to vyřešit pomocí matematiky.

Kanoodle 3-D logická hra
$8.79
S pouhými 12 kousky, ale 200 celkovými výzvami, bude Kanoodle pařezovat děti i dospělé s 2-D a 3-D puzzle.

Desková hra Sagrada
$29.98
V jedné z nejlepších puzzle stolní hry roku, vy a až další tři hráči se pokoušíte vyrobit vitráže oken Sagrada Familia.

Dimension 3-D logická hra
$40.97
Tato logická hra s rychlým tempem 3-D zahrnuje kombinaci rychlého myšlení, logiky a štěstí, abyste mohli nashromáždit své koule a získat co nejvíce bodů.
Z:Populární mechanika


